class methods
- ofVec3f()
- align()
- alignRad()
- angle()
- angleRad()
- average()
- cross()
- distance()
- dot()
- getCrossed()
- getInterpolated()
- getLimited()
- getMapped()
- getMiddle()
- getNormalized()
- getPerpendicular()
- getPtr()
- getRotated()
- getRotatedRad()
- getScaled()
- interpolate()
- isAligned()
- isAlignedRad()
- length()
- limit()
- map()
- match()
- middle()
- normalize()
- one()
- operator!=()
- operator*()
- operator*=()
- operator+()
- operator+=()
- operator-()
- operator-=()
- operator/()
- operator/=()
- operator==()
- operator[]()
- perpendicular()
- rotate()
- rotateRad()
- scale()
- set()
- squareDistance()
- zero()
variables
ofVec3f is a class for storing a three dimensional vector.
Moving through space requires knowledge of where things are and where they are going. Vector Maths is the class of mathematics that gives us control over these things in space, allowing for elegant and intuitive descriptions of complex structures and movement. Vectors are at the heart of animations, particle systems, and 2D and 3D graphics.
Vectors in mathematics in general are entities with magnitude (also called length) and direction. A vector whose magnitude is 1 (ie a vector that is normalized) is called a unit vector. Unit vectors are very handy for storing directions as they can be easily scaled up (or down) to represent motion in a particular direction with a particular length.
You will also see the term 'vector' used to describe an array of objects in C++ (such as text strings). Don't let this confuse you, they are quite different: one of them is a mathematical term for a fixed-length list of numbers that you can do mathematical operations on, the other is a C++-specific term that means 'dynamically sizeable array'.
'ofVec3f' has three member variables, 'x', 'y', and 'z', which allow to conveniently store 3D properties of an object such as its position, velocity, or acceleration.
ofVec3f v1; // v1.x is 0, v1.y is 0, v1.z is 0
v1.set(10, 50, 80); // now v1.x is 10, v1.y is 50, v1.z is 80
Using 'ofVec3f' greatly simplifies arithmetic operations in three dimensions. For example if you have two vectors 'v1' and 'v2', both of which represent a 3D change in position, you can find the total change of position of both of them just by doing an addition 'v1 + v2':
ofVec3f v1(5, 2, 1);
// so now v1 represents walking 5 steps forward then 2 steps
// sideways then 1 step upwards
ofVec3f v2;
v2.set(1, 1, 1);
// so now v2 represents walking 1 step forward then 1 step
// sideways then 1 step upwards
// what happens if you do v1 followed by v2?
// to find out just add v1 and v2 together:
ofVec3f result = v1 + v2;
// result is (6, 3, 1), or 6 steps forward then 3 steps sideways
// then 2 steps upwards
You can scale an 'ofVec3f' by multiplying it with a float:
// walk 5 steps forward then 2 steps sideways then 1 step upwards
ofVec3f v1(5, 2, 1);
// what happens if we do v1 three times?
ofVec3f result = v1 * 3; // result is (15, 6, 3), or
// 15 steps forward, 6 steps sideways and 3 steps upwards
This also works for subtraction and division.
As you can see this really makes dealing with vectors as easy as dealing with single 'float's or 'int's, and can reduce the number of lines of code you have to write by half, at the same time making your code much easier to read and understand!
ofVec3f()
ofVec3f::ofVec3f()
ofVec3f(...)
ofVec3f::ofVec3f(const ofVec4f &vec)
ofVec3f(...)
ofVec3f::ofVec3f(float scalar)
Documentation from code comments
Construct a 3D vector with x, y and z set to scalar
ofVec3f(...)
ofVec3f::ofVec3f(float x, float y, float z)
Construct a 3D vector. Defaults to (0,0).
ofVec3f v1; // default: v1.x is 0, v1.y is 0, v1.z is 0
ofVec3f v2 = ofVec3f(40, 20, 10); // v2.x is 40, v2.y is 20, v2.z is 10
ofVec3f v3(0.1, 0.3, -1.5); // v3.x is 0.1, v3.y is 0.3, v3.z is -1.5
Documentation from code comments
Construt a 3D vector with x, y and z specified
align(...)
bool ofVec3f::align(const ofVec3f &vec, float tolerance=0.0001f)
alignRad(...)
bool ofVec3f::alignRad(const ofVec3f &vec, float tolerance=0.0001f)
angle(...)
float ofVec3f::angle(const ofVec3f &vec)
angleRad(...)
float ofVec3f::angleRad(const ofVec3f &vec)
average(...)
ofVec3f & ofVec3f::average(const ofVec3f *points, int num)
Sets this vector to be the average (centre of gravity or centroid) of a given array of 'ofVec3f's. 'points' is the array of 'ofVec3f's and 'num' specifies the number of 'ofVec3f's in the array.
int numPoints = 10;
ofVec3f points[numPoints];
for ( int i=0; i<numPoints; i++ ) {
points[i].set( ofRandom(0,100), ofRandom(0,100), ofRandom(0,100) );
}
ofVec3f centroid;
centroid.average( points, numPoints );
// centroid now is the centre of gravity/average of all the random points
cross(...)
ofVec3f & ofVec3f::cross(const ofVec3f &vec)
Set this vector to the cross product (vector product) of itself and 'vec'. This is a binary operation on two vectors in three-dimensional space, which results in a vector that is perpendicular to both of the vectors being multiplied, and normal to the plane containing them. The name cross product is derived from the cross symbol X that is often used to designate this operation; the alternative name vector product emphasizes the vector (rather than scalar) nature of the result.
distance(...)
float ofVec3f::distance(const ofVec3f &pnt)
Treats both this vector and 'pnt' as points in 3D space, and calculates and returns the distance between them.
ofVec3f p1(3, 4, 2);
ofVec3f p2(6, 8, 5);
float distance = p1.distance( p2 ); // distance is 5.8310
'distance' involves a square root calculation, which is one of the slowest things you can do in programming. If you don't need an exact number but rather just a rough idea of distance (for example when finding the shortest distance of a bunch of points to a reference point, where it doesn't matter exactly what the distances are, you just want the shortest), you can use 'squareDistance' instead.
dot(...)
float ofVec3f::dot(const ofVec3f &vec)
Calculate and return the dot product of this vector with 'vec'.
Dot product (less commonly known as Euclidean inner product) expresses the angular relationship between two vectors. In other words it is a measure of how parallel two vectors are. If they are completely perpendicular the dot product is 0; if they are completely parallel their dot product is either 1 if they are pointing in the same direction, or -1 if they are pointing in opposite directions.
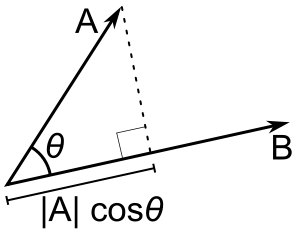 Image courtesy of Wikipedia
Image courtesy of Wikipedia
ofVec3f a1(1, 0, 0);
ofVec3f b1(0, 0, 1); // 90 degree angle to a1
dot = a1.dot(b1); // dot is 0, ie cos(90)
ofVec3f a2(1, 0, 0);
ofVec3f b2(1, 1, 0); // 45 degree angle to a2
b2.normalize(); // vectors should to be unit vectors (normalized)
float dot = a2.dot(b2); // dot is 0.707, ie cos(45)
ofVec3f a3(0, 1, 0);
ofVec3f b3(0, -1, 0); // 180 degree angle to a3
dot = a3.dot(b3); // dot is -1, ie cos(180)
Documentation from code comments
Returns the dot product of this vector with 'vec'.
The dot product of two vectors, also known as the scalar product, is the product of the magnitude of the two vectors and the cosine of the angle between them.
One interpretation of the dot product is as a measure of how closely two vectors align with each other. If they point in exactly the same direction, their dot product will simply be the product of their magnitudes, if they are perpendicular, their dot product will be 0, and if they point in opposite directions, their dot product will be negative.
The dot product is in contrast to the cross product, which returns a vector rather than a scalar.
ofVec3f a1(2, 0, 0); // magnitude 2, parallel to x-axis
ofVec3f b1(3, 4, 0); // magnitude 5, 53.13 degree angle to a1
float dot = a1.dot(b1); // dot is 2 * 5 * cos(53.13) = 6.0
ofVec3f a2(1, 0, 0); // magnitude 1, parallel to x-axis
ofVec3f b2(0, 0, 1); // magnitude 1, 90 degree angle to a2
dot = a2.dot(b2); // dot is 1 * 1 * cos(90) = 0.0
ofVec3f a3(0, 1, 0); // magnitude 1, parallel to y-axis
ofVec3f b3(0, -1, 0); // magnitude 1, 180 degree angle to a3
dot = a3.dot(b3); // dot is 1 * 1 * cos(180) = -1.0
getCrossed(...)
ofVec3f ofVec3f::getCrossed(const ofVec3f &vec)
Returns the cross product (vector product) of this vector and 'vec'. This is a binary operation on two vectors in three-dimensional space, which results in a vector that is perpendicular to both of the vectors being multiplied, and normal to the plane containing them. The name cross product is derived from the cross symbol X that is often used to designate this operation; the alternative name vector product emphasizes the vector (rather than scalar) nature of the result.
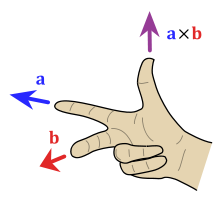 Image courtesy of Wikipedia
Image courtesy of Wikipedia
getInterpolated(...)
ofVec3f ofVec3f::getInterpolated(const ofVec3f &pnt, float p)
Perform a linear interpolation of this vector's position towards 'pnt' and return the interpolated vector without altering the original. 'p' controls the amount to move towards 'pnt'. 'p' is normally between 0 and 1 and where 0 means stay the original position and 1 means move all the way to 'pnt', but you can also have 'p' greater than 1 overshoot 'pnt', or less than 0 to move backwards away from 'pnt'.
ofVec3f v1(0, 5, 0);
ofVec3f v2(10, 10, 20);
ofVec3f v3 = v1.getInterpolated(p2, 0.5); // v3 is (5, 7.5, 10)
ofVec3f v4 = v1.getInterpolated(p2, 0.8); // v4 is (8, 9, 16)
getLimited(...)
ofVec3f ofVec3f::getLimited(float max)
Return a copy of this vector with its length (magnitude) restricted to a maximum of 'max' units by scaling down if necessary.
ofVec3f v1(5, 0, 1); // length is about 5.1
ofVec3f v2(2, 0, 1); // length is about 2.2
ofVec3f v1Limited = v1.getLimited(3);
// v1Limited is (2.9417, 0, 0.58835) which has length of 3 in the same direction as v1
ofVec3f v2Limited = v2.getLimited(3);
// v2Limited is (2, 0, 1) (same as v2)
getMapped(...)
ofVec3f ofVec3f::getMapped(const ofVec3f &origin, const ofVec3f &vx, const ofVec3f &vy, const ofVec3f &vz)
Return a new 'ofVec3f' calculated by copying this vector and then mapping from its default coordinate system -- origin (0,0,0), X direction (1,0,0), Y direction (0,1,0), Z direction (0,0,1) -- to a new coordinate system defined with origin at 'origin', X direction 'vx', and Y direction 'vy', and Z direction 'vz'.
In most cases you want 'vx', 'vy', and 'vz' to be perpendicular and of unit length; if they are not perpendicular you will have shearing as part of the mapping, and if they are not of unit length you will have scaling as part of the mapping.
getMiddle(...)
ofVec3f ofVec3f::getMiddle(const ofVec3f &pnt)
getNormalized()
ofVec3f ofVec3f::getNormalized()
Return a normalized copy of this vector.
Normalization means to scale the vector so that its length (magnitude) is exactly 1, at which stage all that is left is the direction. A normalized vector is usually called a unit vector, and can be used to represent a pure direction (heading).
ofVec3f v1(5, 0, 0);
ofVec3f v1Normalized = v1.getNormalized(); // (1, 0, 0)
ofVec3f v2(5, 0, 5);
ofVec3f v2Normalized = v2.getNormalized(); // (√2, 0, √2)
getPerpendicular(...)
ofVec3f ofVec3f::getPerpendicular(const ofVec3f &vec)
Construct a plane using this vector and 'vec' (by finding the plane that both lectors lie on), and return the vector that is perpendicular to that plane (the normal to that plane).
ofSetLogLevel(OF_LOG_NOTICE);
ofVec3f v1(1,0,0);
ofVec3f v2(0,1,0);
ofVec3f p = v1.getPerpendicular(v2);
ofLog(OF_LOG_NOTICE, "%1.1f, %1.1f, %1.1f\n", p.x, p.y, p.z);
// prints "0.0, 0.0, 1.0"
This method is usually used to calculate a normal vector to a surface, which can then be used to calculate lighting, collisions, and other 3D effects.
getPtr()
float * ofVec3f::getPtr()
Documentation from code comments
Returns a pointer to the memory position of the first element of the vector ('x'); the other elements ('y' and 'z') immediately follow it in memory.
ofVec3f v1 = ofVec3f(40, 20, 10);
float * v1Ptr = v1.getPtr();
float x = *(v1Ptr); // x is 40
float y = *(v1Ptr+1); // y is 20
float z = *(v1Ptr+2); // z is 10
This is very useful when using arrays of 'ofVec3f's to store geometry information, as it allows the vector to be treated as a simple C array of 'float's that can be passed verbatim to OpenGL.
getRotated(...)
ofVec3f ofVec3f::getRotated(float angle, const ofVec3f &axis)
Return a new 'ofVec3f' that is the result of rotating this vector by 'angle' degrees around the given axis.
ofVec3f v1(1, 0, 0);
// rotate v1 around the z axis
ofVec3f v2 = v1.getRotated(45, ofVec3f(0, 0, 1)); // v2 is (√2, √2, 0)
// rotate v1 around the y axis
ofVec3f v3 = v1.getRotated(45, ofVec3f(0, 1, 0)); // v3 is (√2, 0, √2)
getRotated(...)
ofVec3f ofVec3f::getRotated(float ax, float ay, float az)
Make a copy of this vector and perform an Euler rotation of the copy around three axes: 'ax' degrees about the x axis, 'ay' about the y axis and 'az' about the z axis. Return the copy.
ofVec3f v1( 1, 0, 0 );
ofVec3f v2 = v1.getRotated( 0, 0, 90 ); // v is now (0, 1, 0)
ofVec3f v3 = v1.getRotated( 45, 0, 0 ); // v is now (0, √2, √2)
Watch out for gimbal lock when specifying multiple rotations in the same call.
getRotatedRad(...)
ofVec3f ofVec3f::getRotatedRad(float angle, const ofVec3f &axis)
Return a new 'ofVec3f' that is the result of rotating this vector by 'angle' radians around the given axis.
ofVec3f v1(1, 0, 0);
// rotate v1 around the z axis
ofVec3f v2 = v1.getRotated(PI/4, ofVec3f(0, 0, 1)); // v2 is (√2, √2, 0)
// rotate v1 around the y axis
ofVec3f v3 = v1.getRotated(PI/4, ofVec3f(0, 1, 0)); // v3 is (√2, 0, √2)
getRotatedRad(...)
ofVec3f ofVec3f::getRotatedRad(float angle, const ofVec3f &pivot, const ofVec3f &axis)
Return a new 'ofVec3f' that is the result of rotating this vector by 'angle' radians around the axis specified by 'axis', using 'pivot' as the origin of rotation.
getRotatedRad(...)
ofVec3f ofVec3f::getRotatedRad(float ax, float ay, float az)
Make a copy of this vector and perform an Euler rotation of the copy around three axes: 'ax' radians about the x axis, 'ay' about the y axis and 'az' about the z axis. Return the copy.
ofVec3f v1( 1, 0, 0 );
ofVec3f v2 = v1.getRotatedRad( 0, 0, HALF_PI ); // v is now (0, 1, 0)
ofVec3f v3 = v1.getRotatedRad( PI/4, 0, 0 ); // v is now (0, √2, √2)
Watch out for gimbal lock when specifying multiple rotations in the same call.
getScaled(...)
ofVec3f ofVec3f::getScaled(const float length)
interpolate(...)
ofVec3f & ofVec3f::interpolate(const ofVec3f &pnt, float p)
Perform a linear interpolation of this vector's position towards 'pnt'. 'p' controls the amount to move towards 'pnt'. 'p' is normally between 0 and 1 and where 0 means stay the original position and 1 means move all the way to 'pnt', but you can also have 'p' greater than 1 overshoot 'pnt', or less than 0 to move backwards away from 'pnt'.
ofVec3f v1( 0, 5, 0 );
ofVec3f v2( 10, 10, 20 );
// go go gadget zeno
v1.interpolate( v2, 0.5 ); // v1 is now (5, 7.5, 10)
v1.interpolate( v2, 0.5 ); // v1 is now (7.5, 8.75, 15)
v1.interpolate( v2, 0.5 ); // v1 is now (8.75, 9.375, 17.5)
v1.interpolate( v2, 0.5 ); // v1 is now (9.375, 9.6875, 18.75)
isAligned(...)
bool ofVec3f::isAligned(const ofVec3f &vec, float tolerance=0.0001f)
Documentation from code comments
/ Checks if vectors look in the same direction. /
length()
float ofVec3f::length()
Return the length (magnitude) of this vector.
ofVec3f v(3, 4, 1);
float len = v.length(); // len is 5.0990
'length' involves a square root calculation, which is one of the slowest things you can do in programming. If you don't need an exact number but rather just a rough idea of a length (for example when finding the shortest distance of a bunch of points to a reference point, where it doesn't matter exactly what the lengths are, you just want the shortest), you can use 'squareLength' instead.
limit(...)
ofVec3f & ofVec3f::limit(float max)
Restrict the length (magnitude) of this vector to a maximum of 'max' units by scaling down if necessary.
ofVec3f v1(5, 0, 1); // length is about 5.1
ofVec3f v2(2, 0, 1); // length is about 2.2
v1.limit(3);
// v1 is now (2.9417, 0, 0.58835) which has length of 3 in the same direction as at initialization
v2.limit(3);
// v2 is unchanged
map(...)
ofVec3f & ofVec3f::map(const ofVec3f &origin, const ofVec3f &vx, const ofVec3f &vy, const ofVec3f &vz)
Map this vector from its default coordinate system -- origin (0,0,0), X direction (1,0,0), Y direction (0,1,0), Z direction (0,0,1) -- to a new coordinate system defined with origin at 'origin', X direction 'vx', and Y direction 'vy', and Z direction 'vz'.
In most cases you want 'vx', 'vy', and 'vz' to be perpendicular and of unit length; if they are not perpendicular you will have shearing as part of the mapping, and if they are not of unit length you will have scaling as part of the mapping.
match(...)
bool ofVec3f::match(const ofVec3f &vec, float tolerance=0.0001f)
middle(...)
ofVec3f & ofVec3f::middle(const ofVec3f &pnt)
Set this vector to the midpoint between itself and 'pnt'.
ofVec3f v1( 0, 5, 0 );
ofVec3f v2( 10, 10, 20);
// go go gadget zeno
v1.middle( v2 ); // v1 is now (5, 7.5, 10)
v1.middle( v2 ); // v1 is now (7.5, 8.75, 15)
v1.middle( v2 ); // v1 is now (8.75, 9.375, 17.5)
v1.middle( v2 ); // v1 is now (9.375, 9.6875, 18.75)
normalize()
ofVec3f & ofVec3f::normalize()
Normalize the vector.
Normalizing means to scale the vector so that its length (magnitude) is exactly 1, at which stage all that is left is the direction. A normalized vector is usually called a unit vector, and can be used to represent a pure direction (heading).
ofVec3f v1(5, 0, 0);
v1.normalize(); // v2 is now (1, 0, 0)
ofVec3f v2(5, 0, 5);
v2.normalize(); // v2 is now (√2, 0, √2)
operator!=(...)
bool ofVec3f::operator!=(const ofVec3f &vec)
operator*(...)
ofVec3f ofVec3f::operator*(const float f)
operator*(...)
ofVec3f ofVec3f::operator*(const ofVec3f &vec)
operator*=(...)
ofVec3f & ofVec3f::operator*=(const float f)
Scale this vector by multiplying 'x', 'y' and 'z' members by 'f'.
ofVec3f v1(2, 5, 1);
v1 *= 4; // (8, 20, 4)
operator*=(...)
ofVec3f & ofVec3f::operator*=(const ofVec3f &vec)
operator+(...)
ofVec3f ofVec3f::operator+(const float f)
operator+(...)
ofVec3f ofVec3f::operator+(const ofVec3f &pnt)
operator+=(...)
ofVec3f & ofVec3f::operator+=(const float f)
Adds a float value 'f' to 'x', 'y' and 'z' members.
ofVec3f v1(2, 5, 1);
v1 += 10; // (12, 15, 11)
operator+=(...)
ofVec3f & ofVec3f::operator+=(const ofVec3f &pnt)
operator-()
ofVec3f ofVec3f::operator-()
operator-(...)
ofVec3f ofVec3f::operator-(const float f)
operator-(...)
ofVec3f ofVec3f::operator-(const ofVec3f &vec)
operator-=(...)
ofVec3f & ofVec3f::operator-=(const float f)
Subtract a float value 'f' from 'x', 'y', and 'z' members.
ofVec3f v1(2, 5, 1);
v1 -= 10; // (-8, -5, -9)
operator-=(...)
ofVec3f & ofVec3f::operator-=(const ofVec3f &vec)
operator/(...)
ofVec3f ofVec3f::operator/(const float f)
operator/(...)
ofVec3f ofVec3f::operator/(const ofVec3f &vec)
operator/=(...)
ofVec3f & ofVec3f::operator/=(const float f)
Scale this vector by dividing 'x', 'y' and 'z' members by 'f'.
ofVec3f v1(2, 5, 1);
v1 /= 4; // (0.5, 1.25, 0.25)
operator/=(...)
ofVec3f & ofVec3f::operator/=(const ofVec3f &vec)
operator==(...)
bool ofVec3f::operator==(const ofVec3f &vec)
Returns 'true' if each component is the same as the corresponding component in 'vec', ie if 'x == vec.x' and 'y == vec.y' and 'z == vec.z'; otherwise returns 'false'. But you should probably be using 'match' instead.
ofVec3f v1(40, 20, 10);
ofVec3f v2(50, 30, 10);
ofVec3f v3(40, 20, 10);
// ( v1 == v2 ) is false
// ( v1 == v3 ) is true
operator[](...)
float & ofVec3f::operator[](int n)
Documentation from code comments
Allows to access the individual components of an 'ofVec3f' as though it is an array
ofVec3f v1 = ofVec3f(40, 20, 10);
float x = v1[0]; // x is 40
float y = v1[1]; // y is 20
float z = v1[2]; // z is 10
This function can be handy if you want to do the same operation to all 'x', 'y' and 'z' components, as it means you can just make a 'for' loop that repeats 3 times.
perpendicular(...)
ofVec3f & ofVec3f::perpendicular(const ofVec3f &vec)
Construct a plane using this vector and 'vec' (by finding the plane that both lie on), and set our 'x', 'y' and 'z' to be the vector that is perpendicular to the constructed plane (the normal to the plane).
ofSetLogLevel(OF_LOG_NOTICE);
ofVec3f v1(1,0,0);
ofVec3f v2(0,1,0);
v1.perpendicular(v2);
ofLog(OF_LOG_NOTICE, "%1.1f, %1.1f, %1.1f\n", v1.x, v1.y, v1.z);
// prints "0.0, 0.0, 1.0'
This method is usually used to calculate a normal vector to a surface, which can then be used to calculate lighting, collisions, and other 3D effects.
rotate(...)
ofVec3f & ofVec3f::rotate(float angle, const ofVec3f &axis)
Return a new 'ofVec3f' that is the result of rotating this vector by 'angle' degrees around the given axis.
ofVec3f v1(1, 0, 0);
// rotate v1 around the z axis
v1.rotate(45, ofVec3f(0, 0, 1)); // v2 is (√2, √2, 0)
v1.set(1, 0, 0);
// then rotate around the y axis
v1.rotate(45, ofVec3f(0, 1, 0)); // v3 is (√2, 0, √2)
rotate(...)
ofVec3f & ofVec3f::rotate(float angle, const ofVec3f &pivot, const ofVec3f &axis)
Rotate this vector by 'angle' degrees around the axis specified by 'axis', using 'pivot' as the origin of rotation.
rotate(...)
ofVec3f & ofVec3f::rotate(float ax, float ay, float az)
Perform an Euler rotation of this vector around three axes: 'ax' degrees about the x axis, 'ay' about the y axis and 'az' about the z axis.
ofVec3f v( 1, 0, 0 );
v.rotate( 0, 0, 90 ); // v is now (0, 1, 0)
v.rotate( 45, 0, 0 ); // v is now (0, √2, √2)
Watch out for gimbal lock when specifying multiple rotations in the same call.
rotateRad(...)
ofVec3f & ofVec3f::rotateRad(float angle, const ofVec3f &axis)
Return a new 'ofVec3f' that is the result of rotating this vector by 'angle' degrees around the given axis.
ofVec3f v1(1, 0, 0);
// rotate v1 around the z axis
v1.rotate(45, ofVec3f(0, 0, 1)); // v2 is (√2, √2, 0)
v1.set(1, 0, 0);
// then rotate around the y axis
v1.rotate(45, ofVec3f(0, 1, 0)); // v3 is (√2, 0, √2)
rotateRad(...)
ofVec3f & ofVec3f::rotateRad(float angle, const ofVec3f &pivot, const ofVec3f &axis)
Rotate this vector by 'angle' radians around the axis specified by 'axis', using 'pivot' as the origin of rotation.
rotateRad(...)
ofVec3f & ofVec3f::rotateRad(float ax, float ay, float az)
Perform an Euler rotation of this vector around three axes: 'ax' radians about the x axis, 'ay' about the y axis and 'az' about the z axis.
ofVec3f v( 1, 0, 0 );
v.rotateRad( 0, 0, HALF_PI ); // v is now (0, 1, 0)
v.rotateRad( PI/4, 0, 0 ); // v is now (0, √2, √2)
Watch out for gimbal lock when specifying multiple rotations in the same call.
scale(...)
ofVec3f & ofVec3f::scale(const float length)
Scales this vector up or down so that it has the requested length.
ofVec3f v1(3, 4); // length is 5
v1.scale(15); // v1 is now (9, 12), which has length of 15
set(...)
void ofVec3f::set(const ofVec3f &vec)
set(...)
void ofVec3f::set(float x, float y, float z)
Set 'x', 'y' and 'z' components of this vector with just one function call. 'z' is optional, it defaults to 0.
ofVec3f v1;
v1.set(40, 20, 70);
squareDistance(...)
float ofVec3f::squareDistance(const ofVec3f &pnt)
Treats both this vector and 'pnt' as points in 3D space, and calculates and returns the squared distance between them.
ofVec3f p1(3, 4, 2);
ofVec3f p2(6, 8, 5);
float distance = p1.distance( p2 ); // distance is 5.8310
Use as a much faster alternative to 'distance' if you don't need to know an exact number but rather just a rough idea of distance (for example when finding the shortest distance of a bunch of points to a reference point, where it doesn't matter exactly what the distances are, you just want the shortest). It avoids the square root calculation that is ordinarily required to calculate a length.
Last updated Friday, 02 May 2025 18:57:28 UTC - 0cfbc5eb74e8f627fe4da3fb60a3ee56ee64a172


If you have any doubt about the usage of this module you can ask in the forum.
If you want to contribute better documentation or start documenting this section you can do so here
If you find anything wrong with this docs you can report any error by opening an issue