class methods
- ofPolyline_()
- addVertex()
- addVertices()
- arc()
- arcNegative()
- begin()
- bezierTo()
- clear()
- close()
- curveTo()
- draw()
- end()
- flagHasChanged()
- fromRectangle()
- getArea()
- getBoundingBox()
- getCentroid2D()
- getClosestPoint()
- getDegreesAtIndex()
- getDegreesAtIndexInterpolated()
- getIndexAtLength()
- getIndexAtPercent()
- getLengthAtIndex()
- getLengthAtIndexInterpolated()
- getNormalAtIndex()
- getNormalAtIndexInterpolated()
- getPerimeter()
- getPointAtIndexInterpolated()
- getPointAtLength()
- getPointAtPercent()
- getRadiansAtIndex()
- getRadiansAtIndexInterpolated()
- getResampledByCount()
- getResampledBySpacing()
- getRightVector()
- getRotationAtIndex()
- getRotationAtIndexInterpolated()
- getSmoothed()
- getTangentAtIndex()
- getTangentAtIndexInterpolated()
- getVertices()
- getWrappedIndex()
- hasChanged()
- insertVertex()
- inside()
- isClosed()
- lineTo()
- operator[]()
- quadBezierTo()
- rbegin()
- rend()
- resize()
- rotateDeg()
- rotateRad()
- scale()
- setClosed()
- setRightVector()
- simplify()
- size()
- translate()
global functions
ofPolyLine allows you to combine multiple points into a single vector data object that can be drawn to the screen, manipulated point by point, and combined with other ofPolyline instances. It is less complex than the ofPath and generally represents a single line or vector shape rather than multiple lines or shapes.
You can add points to an ofPolyline by adding vertices. By default these vertices are ofVec3f types, meaning you also need to specify a z-value, even when drawing in 2D:
float i = 0;
while (i < TWO_PI) { // make a heart
float r = (2-2*sin(i) + sin(i)*sqrt(abs(cos(i))) / (sin(i)+1.4)) * -80;
float x = ofGetWidth()/2 + cos(i) * r;
float y = ofGetHeight()/2 + sin(i) * r;
line.addVertex(ofVec3f(x,y,0));
i+=0.005*HALF_PI*0.5;
}
line.close(); // close the shape
or you can draw lines or curves:
float angle = 0;
while (angle < TWO_PI ) {
b.curveTo(100*cos(angle), 0, 100*sin(angle));
b.curveTo(300*cos(angle), 300, 300*sin(angle));
angle += TWO_PI / 30;
}
ofPolyline also includes methods to get the closest point, determine whether a point is inside shape, and resample shapes. Along with the ofPath class, it's the best way to draw and manipulate 2D and 3D vector graphics that you'll need to update and manipulate frequently.
If you use the lineTo or curveTo or bezierTo functions, you move the drawing point, so that drawing a line to 100,100 means a line from 0,0 to 100, 100. The next line would be a line from 100,100 to wherever you go next. Storing this position means that you can easily create continuous drawings without difficulty.
ofPolyline_(...)
ofPolyline_::ofPolyline_(const vector< T > &verts)
Creates an ofPolyline from a vector of ofVec2f or ofPoint objects.
vector<ofPoint> pts;
float j = 0;
while(j < TWO_PI+0.1) {
pts.push_back( ofPoint(cos(j) * 100, sin(j) * 100));
j+=0.1;
}
ofPolyline cp(pts);
There is an easier way to draw circles though, using the arc() method.
addVertex(...)
void ofPolyline_::addVertex(const T &p)
Adds a point using an ofPoint at the end of the ofPolyline.
Documentation from code comments
Adds a point using an T at the end of the ofPolyline.
addVertex(...)
void ofPolyline_::addVertex(float x, float y, float z)
Adds a point using floats instead of an ofPoint at the end of the ofPolyline.
Documentation from code comments
Adds a point using floats at the end of the ofPolyline.
addVertices(...)
void ofPolyline_::addVertices(const T *verts, int numverts)
Adds multiple points at the end of the ofPolyline using a pointer to an array of ofPoint objects.
ofPoint* verts = new ofPoint[5];
// make a pentagon
float size = 80.f;
float X1 = 0.125*sqrt(10 + 2*sqrt(5)) * size;
float X2 = 0.125*sqrt(10 - 2*sqrt(5)) * size;
float Y1 = 0.125*(sqrt(5) - 1) * size;
float Y2 = 0.125*(sqrt(5) + 1) * size;
verts[0] = ofPoint(0, -0.5 * size);
verts[1] = ofPoint(-X1, -Y1);
verts[2] = ofPoint(-X2, Y2);
verts[3] = ofPoint(X2, Y2);
verts[4] = ofPoint(X1, -Y1);
ofPolyline p;
p.addVertices(verts, 5);
Documentation from code comments
Adds multiple points at the end of the ofPolyline using a pointer to an array of T objects.
addVertices(...)
void ofPolyline_::addVertices(const vector< T > &verts)
Documentation from code comments
Add multiple points at the end of the ofPolyline using a vector of T objects
// make a pentagon
float size = 80.f;
float X1 = 0.125*sqrt(10 + 2*sqrt(5)) * size;
float X2 = 0.125*sqrt(10 - 2*sqrt(5)) * size;
float Y1 = 0.125*(sqrt(5) - 1) * size;
float Y2 = 0.125*(sqrt(5) + 1) * size;
vector<T> verts = {
{0, -0.5 * size, 0.f),
{-X1, -Y1, 0.f},
{-X2, Y2, 0.f},
{X2, Y2, 0.f},
{X1, -Y1, 0.f},
};
ofPolyline p;
p.addVertices(verts);
arc(...)
void ofPolyline_::arc(const T ¢er, float radiusX, float radiusY, float angleBegin, float angleEnd, bool clockwise, int circleResolution=20)
Draws an arc around the ofPoint center with the width of radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of the arc in degrees measured clockwise from the x-axis.
The clockwise boolean sets the drawing direction. Passing 'false' to it will draw the arc counter-clockwise.
Optionally, you can specify circleResolution, which is the number of line segments a circle would be drawn with.
arc(...)
void ofPolyline_::arc(const T ¢er, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)
Draws an arc around the ofPoint center with the width of radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number of line segments a circle would be drawn with.
A partial arc will be drawn with the same resolution: if circleResolution == 20, a half-circle will be drawn with 10 segments.
If there are already vertices in the ofPolyline the arc will extend them; a line will be created from the endmost point on the ofPolyline to the beginning point of the arc.
Example:
ofPolyline polyline1, polyline2;
// draw an circle with a diameter of 100 in blue
ofPoint point1(150,120);
polyline1.arc(point1,100,100,0,360);
ofSetColor(ofColor::blue);
polyline1.draw();
// draw an line, then an semi-circle in red
polyline2.lineTo(300, 50);
ofPoint point2(450,120);
polyline2.arc(point2,100,100,0,180);
ofSetColor(ofColor::red);
polyline2.draw();

arc(...)
void ofPolyline_::arc(float x, float y, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)
Draws an arc around the coordinates (x,y) with the width of radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number of line segments a circle would be drawn with.
arc(...)
void ofPolyline_::arc(float x, float y, float z, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)
Draws an arc around the coordinates (x,y,z) with the width of radiusX and the height of radiusY.
The angleBegin and angleEnd indicate the start and end angles of the arc in degrees measured clockwise from the x-axis.
Optionally, you can specify circleResolution, which is the number of line segments a circle would be drawn with.
arcNegative(...)
void ofPolyline_::arcNegative(const T ¢er, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)
arcNegative(...)
void ofPolyline_::arcNegative(float x, float y, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)
arcNegative(...)
void ofPolyline_::arcNegative(float x, float y, float z, float radiusX, float radiusY, float angleBegin, float angleEnd, int circleResolution=20)
bezierTo(...)
void ofPolyline_::bezierTo(const T &cp1, const T &cp2, const T &to, int curveResolution=20)
Creates a cubic bezier line from the current drawing point with the 2 control points indicated by ofPoint cp1 and cp2, that ends at ofPoint to. For instance, the following:
line.addVertex(ofPoint(200, 400));
line.bezierTo(100, 100, 800, 100, 700, 400);
Creates this:
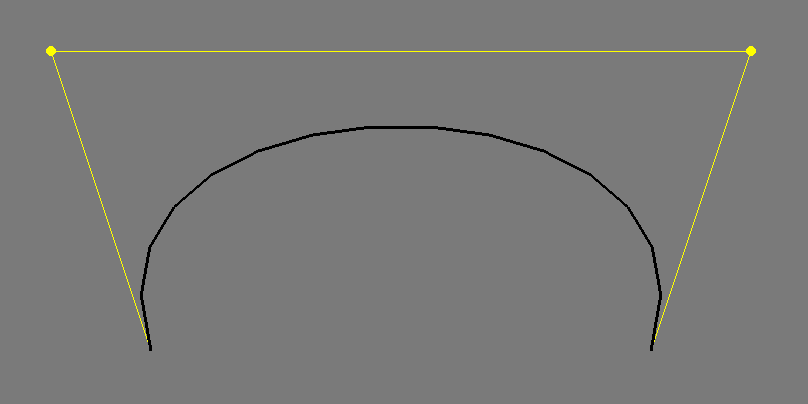 The control points are shown in yellow.
The control points are shown in yellow.
Documentation from code comments
Adds a cubic bezier line from the current drawing point with the 2 control points indicated by T cp1 and cp2, that ends at T to.
line.addVertex(T(200, 400));
line.bezierTo(100, 100, 800, 100, 700, 400);
 The control points are shown in red.
The control points are shown in red.
bezierTo(...)
void ofPolyline_::bezierTo(float cx1, float cy1, float cx2, float cy2, float x, float y, int curveResolution=20)
Creates a cubic bezier line from the current drawing point with the 2 control points indicated by the coordinates cx1, cy1 and cx2, cy2, that ends at the coordinates x, y.
bezierTo(...)
void ofPolyline_::bezierTo(float cx1, float cy1, float cz1, float cx2, float cy2, float cz2, float x, float y, float z, int curveResolution=20)
Creates a cubic bezier line in 3D space from the current drawing point with the 2 control points indicated by the coordinates cx1, cy1, cz1 and cx2, cy2, cz2, that ends at the coordinates x, y, z.
float cx = ofGetWidth()/2;
float cy = 200;
float step = TWO_PI / 60;
for (float i = 0.0; i < TWO_PI; i+=step) {
if(i == 0.0) {
line.addVertex(cx + (400*cos(i)), cy+400, 400 * sin(i));
} else {
line.bezierTo( cx - (200*cos(i)), cy-100, 400 * sin(i),
cx + (200*cos(i)), cy+600, 400 * sin(i),
cx + (400*cos(i)), cy+400, 400 * sin(i));
}
}
Documentation from code comments
Adds a cubic bezier line in 3D space from the current drawing point with the 2 control points indicated by the coordinates cx1, cy1, cz1 and cx2, cy2, cz2, that ends at the coordinates x, y, z.
close()
void ofPolyline_::close()
Closes the ofPolyline, meaning that all the vertices will be linked and can be "walked".
curveTo(...)
void ofPolyline_::curveTo(const T &to, int curveResolution=20)
Draws a curve to an ofPoint object passed in:
float angle = 0;
while (angle < TWO_PI ) {
b.curveTo( ofPoint(100*cos(angle), 100*sin(angle)));
b.curveTo( ofPoint(300*cos(angle), 300*sin(angle)));
angle += TWO_PI / 30;
}
You need at least 4 points to be able to draw with curveTo, here's an explanation of why this happens:
If we have an empty ofPolyline p, and we do:
p.lineTo(v0);
p.lineTo(v1);
p.lineTo(v2);
p.lineTo(v3);
We end up with a line that starts at v0, heads to v1, then heads to v2 and finally ends at v3. But if we had instead done:
p.curveTo(v0);
p.curveTo(v1);
p.curveTo(v2);
p.curveTo(v3);
We end up with a curve that goes from v1 to v2. That might seem initially puzzling...
So, we have to dive under the hood. The curveTo(...) method makes Catmull-Rom splines wiki. The relevant bit to understand is that this type of spline is defined by four points:

P1 and P2 are the endpoints of our curve, while P0 and P3 are the control that define the shape of the curve.
When using curveTo(...) with ofPolyline, there's an internal vector that stores P0, P1, P2 and P3. When our ofPolyline is empty then the internal vector is also empty. When we call:
p.curveTo(v0); // Internal vector is [v0], so only P0 is defined
p.curveTo(v1); // Internal vector is [v0, v1], so only P0 and P1 are defined
p.curveTo(v2); // Internal vector is [v0, v1, v2], so only P0, P1 and P2 are defined
p.curveTo(v3); // Internal vector is [v0, v1, v2, v3], so all points are defined
Only once all of those points (P0 through P4) have been defined, then a spline has been fully defined and vertices can finally be added to our ofPolyline. When curveTo(v3) is called above, then the curve between P1 (v1) and P2 (v2) is sampled (at a resolution defined by the optional parameter curveResolution). That sampling slides along the curve and adds vertices to your ofPolyline.
The curve doesn't start at v0 and end at v3 because those points are acting as the control points (i.e. the points connected by dotted lines in the image above).
And now that we have P0 through P4 defined, when we call curveTo(...) next:
curveTo(v4); // Internal vector becomes [v1, v2, v3, v4]
The oldest point, v0, was bumped and everything shifted down. The sampling occurs again, but this time it is between v2 and v3.
Documentation from code comments
Adds a curve to an T object passed in
float angle = 0;
while (angle < TWO_PI ) {
b.curveTo( T(100*cos(angle), 100*sin(angle)));
b.curveTo( T(300*cos(angle), 300*sin(angle)));
angle += TWO_PI / 30;
}
\note You need at least 4 points to be able to use curveTo()
See also: Catmull-Rom splines wiki
curveTo(...)
void ofPolyline_::curveTo(float x, float y, float z, int curveResolution=20)
Draws a curve to the x,y,z points passed in with the optional resolution.
float angle = 0;
while (angle < TWO_PI ) {
polyline.curveTo(100*cos(angle), 0, 100*sin(angle));
polyline.curveTo(300*cos(angle), 300, 300*sin(angle));
angle += TWO_PI / 30;
}
Documentation from code comments
Adds a curve to the x,y,z points passed in with the optional resolution.
getArea()
float ofPolyline_::getArea()
Documentation from code comments
Gets the precise area bounded by the line
getBoundingBox()
ofRectangle ofPolyline_::getBoundingBox()
Documentation from code comments
Get the bounding box of the polyline , taking into account all the points to determine the extents of the polyline.
getCentroid2D()
T ofPolyline_::getCentroid2D()
Documentation from code comments
Get the center of the area bounded by the line
getClosestPoint(...)
T ofPolyline_::getClosestPoint(const T &target, unsigned int *nearestIndex)
Returns the bounding box of the shape, taking into account all the points to determine the extents of the polyline.
Documentation from code comments
Gets the point on the line closest to the target. You can also optionally pass a pointer to/address of an unsigned int to get the index of the closest vertex
getDegreesAtIndex(...)
float ofPolyline_::getDegreesAtIndex(int index)
Get the center of the area bounded by the line.
Documentation from code comments
Get angle (degrees) of the path at index
getDegreesAtIndexInterpolated(...)
float ofPolyline_::getDegreesAtIndexInterpolated(float findex)
This returns the point on the line closest to the target. You can also optionally pass a pointer to/address of an unsigned int to get the index of the closest vertex.
Documentation from code comments
Get angle (degrees) at interpolated index (interpolated between neighboring indices)
getIndexAtLength(...)
float ofPolyline_::getIndexAtLength(float f)
Documentation from code comments
Get (interpolated) index at given length along the path
Includes info on percentage along segment, e.g. ret=5.75 =>
75% along the path between 5th and 6th points
getIndexAtPercent(...)
float ofPolyline_::getIndexAtPercent(float f)
Documentation from code comments
Get (interpolated) index at given percentage along the path
Includes info on percentage along segment, e.g. ret=5.75
=> 75% along the path between 5th and 6th points
getLengthAtIndex(...)
float ofPolyline_::getLengthAtIndex(int index)
Documentation from code comments
Get length along path at index
getLengthAtIndexInterpolated(...)
float ofPolyline_::getLengthAtIndexInterpolated(float findex)
Documentation from code comments
Get length along path at interpolated index (e.g. f=5.75 => 75% along
the path between 5th and 6th points)
getNormalAtIndex(...)
T ofPolyline_::getNormalAtIndex(int index)
Documentation from code comments
Get normal vector at index
getNormalAtIndexInterpolated(...)
T ofPolyline_::getNormalAtIndexInterpolated(float findex)
Documentation from code comments
Get normal vector at interpolated index (interpolated between neighboring indices)
getPerimeter()
float ofPolyline_::getPerimeter()
Documentation from code comments
Gets the size of the perimeter of the polyline, good for determining length of the line, rather than just the bounding box shape.
getPointAtIndexInterpolated(...)
T ofPolyline_::getPointAtIndexInterpolated(float findex)
Documentation from code comments
Get point along the path at interpolated index (e.g. f=5.75 =>
75% along the path between 5th and 6th points)
getPointAtLength(...)
T ofPolyline_::getPointAtLength(float f)
Documentation from code comments
Get point long the path at a given length (e.g. f=150 => 150
units along the path)
getPointAtPercent(...)
T ofPolyline_::getPointAtPercent(float f)
Documentation from code comments
Get point along the path at a given percentage (e.g. f=0.25
=> 25% along the path)
getRadiansAtIndex(...)
float ofPolyline_::getRadiansAtIndex(int index)
Documentation from code comments
Get angle (degrees) of the path at index
getRadiansAtIndexInterpolated(...)
float ofPolyline_::getRadiansAtIndexInterpolated(float findex)
Documentation from code comments
Get angle (degrees) at interpolated index (interpolated between neighboring indices)
getResampledByCount(...)
ofPolyline_< T > ofPolyline_::getResampledByCount(int count)
This resamples the line based on the spacing passed in. The lower the count passed in, the more points will be eliminated. New points are added if necessary to match count.
getResampledBySpacing(...)
ofPolyline_< T > ofPolyline_::getResampledBySpacing(float spacing)
This resamples the line based on the spacing passed in. The larger the spacing, the more points will be eliminated.
line.draw();
ofTranslate(400, 0);
line.getResampledBySpacing(100).draw();

getRotationAtIndex(...)
T ofPolyline_::getRotationAtIndex(int index)
Documentation from code comments
Get rotation vector at index (magnitude is sine of angle)
getRotationAtIndexInterpolated(...)
T ofPolyline_::getRotationAtIndexInterpolated(float findex)
Documentation from code comments
Get rotation vector at interpolated index (interpolated between neighboring indices) (magnitude is sine of angle)
getSmoothed(...)
ofPolyline_< T > ofPolyline_::getSmoothed(int smoothingSize, float smoothingShape)
Documentation from code comments
Gets a smoothed version of the ofPolyline.
smoothingSize is the size of the smoothing window. So if
smoothingSize is 2, then 2 points from the left, 1 in the center,
and 2 on the right (5 total) will be used for smoothing each point.
smoothingShape describes whether to use a triangular window (0) or
box window (1) or something in between (for example, .5).
getTangentAtIndex(...)
T ofPolyline_::getTangentAtIndex(int index)
Documentation from code comments
Get tangent vector at index
getTangentAtIndexInterpolated(...)
T ofPolyline_::getTangentAtIndexInterpolated(float findex)
Documentation from code comments
Get tangent vector at interpolated index (interpolated between neighboring indices)
getVertices()
vector< T > & ofPolyline_::getVertices()
Documentation from code comments
Gets a vector of vertices that the line contains
getWrappedIndex(...)
int ofPolyline_::getWrappedIndex(int index)
Documentation from code comments
Get wrapped index depending on whether poly is closed or not
hasChanged()
bool ofPolyline_::hasChanged()
Documentation from code comments
Returns whether the vertices within the line have changed.
inside(...)
bool ofPolyline_::inside(const T &p)
Tests whether the ofPoint is within a closed ofPolyline.
Documentation from code comments
Tests whether the T is within a closed ofPolyline.
inside(...)
bool ofPolyline_::inside(const T &p, const ofPolyline_< T > &polyline)
Test whether the ofPoint is within anothe polyline, passed in as ofPolyline&
Documentation from code comments
Tests whether the T is within a closed ofPolyline.
inside(...)
bool ofPolyline_::inside(float x, float y)
Tests whether the x,y coordinates are within a closed ofPolyline.
inside(...)
bool ofPolyline_::inside(float x, float y, const ofPolyline_< T > &polyline)
Test whether the x,y point is within anothe polyline, passed in as ofPolyline&
Documentation from code comments
Tests whether the x,y coordinates are within a closed ofPolyline.
lineTo(...)
void ofPolyline_::lineTo(const T &to)
Add a line from the last point added, or from 0,0 if no point is set, to the point indicated by the ofPoint passesd in.
Documentation from code comments
Add a straight line from the last point added, or from 0,0 if no point is set, to the point indicated by the T passesd in.
lineTo(...)
void ofPolyline_::lineTo(float x, float y, float z)
Add a line from the last point added, or from 0,0 if no point is set, to the point indicated by the floats x,y,z passesd in.
operator[](...)
const T & ofPolyline_::operator[](int index)
Documentation from code comments
Allows you to access the points of the ofPolyline just like you would in an array, so to make the points of a line follow the mouse movement, you could do:
line[0].set(mouseX, mouseY);
int i = 1;
while ( i<bounds.size()) {
float angle = atan2(line[i-1].y - line[i].y, line[i-1].x - line[i].x);
bounds[i].set(bounds[i-1].x - cos(angle) * 20, bounds[i-1].y - sin(angle) * 20);
i++;
}
operator[](...)
T & ofPolyline_::operator[](int index)
The [] operator allows you to access the points of the ofPolyline just like you would in an array, so to make the points of a line follow the mouse movement, you could do:
line[0].set(mouseX, mouseY);
int i = 1;
while ( i<bounds.size()) {
float angle = atan2(line[i-1].y - line[i].y, line[i-1].x - line[i].x);
bounds[i].set(bounds[i-1].x - cos(angle) * 20, bounds[i-1].y - sin(angle) * 20);
i++;
}
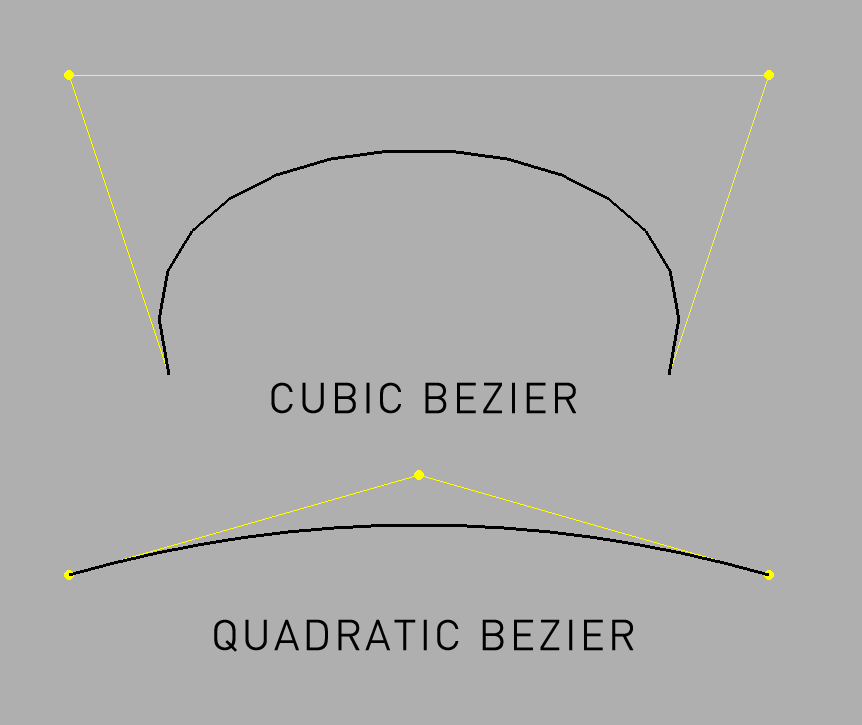
quadBezierTo(...)
void ofPolyline_::quadBezierTo(const T &p1, const T &p2, const T &p3, int curveResolution=20)
Creates a quadratic bezier line in 2D space from the current drawing point with the beginning indicated by the point p1, the control point at p2, and that ends at the point p3.
quadBezierTo(...)
void ofPolyline_::quadBezierTo(float cx1, float cy1, float cx2, float cy2, float x, float y, int curveResolution=20)
Creates a quadratic bezier line in 3D space from the current drawing point with the beginning indicated by the coordinates cx1, cy1, the control point at cx2, cy2, and that ends at the coordinates x, y.
quadBezierTo(...)
void ofPolyline_::quadBezierTo(float cx1, float cy1, float cz1, float cx2, float cy2, float cz2, float x, float y, float z, int curveResolution=20)
Creates a quadratic bezier line in 3D space from the current drawing point with the beginning indicated by the coordinates cx1, cy1, cz1, the control point at cx2, cy2, cz2, and that ends at the coordinates x, y, z.
resize(...)
void ofPolyline_::resize(size_t size)
Documentation from code comments
Resize the number of points in the ofPolyline to the value passed in.
rotateDeg(...)
void ofPolyline_::rotateDeg(float degrees, const glm::vec3 &axis)
Documentation from code comments
} \name Transform polyline {
scale(...)
void ofPolyline_::scale(float x, float y)
Documentation from code comments
Change the size of the ofPolyline These changes are non-reversible, so for instance scaling by 0,0 zeros out all data.
setClosed(...)
void ofPolyline_::setClosed(bool tf)
Documentation from code comments
Closes the ofPolyline, meaning that all the vertices will be linked and can be "walked".
simplify(...)
void ofPolyline_::simplify(float tolerance=0.3f)
Simplifies the polyline, removing un-necessary vertices. The tolerance determines how dis-similar points need to be to stay in the line. Higher tolerance means more points removed, lower tolerance means less points removed.
size()
size_t ofPolyline_::size()
Documentation from code comments
The number of points in the ofPolyline.
ofInsidePoly(...)
bool ofInsidePoly(const T &p, const int &poly)
ofInsidePoly(...)
bool ofInsidePoly(float x, float y, const int &polygon)
Documentation from code comments
Determine if an (x,y) coordinate is within the polygon defined by a vector of glm::vec3s.
Parameters:
x The x dimension of the coordinate.
y The y dimension of the coordinate.
poly a vector of glm::vec3s defining a polygon.
Returns: True if the point defined by the coordinates is enclosed, false otherwise.
Last updated Friday, 05 January 2024 04:30:21 UTC - 76da1a94ddd033ed7b011f01e62bc1521791976d



If you have any doubt about the usage of this module you can ask in the forum.
If you want to contribute better documentation or start documenting this section you can do so here
If you find anything wrong with this docs you can report any error by opening an issue